Room 505, Cosmology Building, NTU
Speaker(s):
Kengo Nakajima (University of Tokyo)
Organizer(s):
Weichung Wang (National Taiwan University)
Tsung-Ming Huang (National Taiwan Normal University)
Feng-Nan Hwang (National Central University)
Pochung Chen (National Tsing Hua University)
Ying-Jer Kao (National Taiwan University)
Yu-Heng Tseng (Institute of Oceanography, National Taiwan University)
1. Course Background & Purposes
Several sample programs will be provided and participants can review the contents of lectures through hands-on-exercise/practices using the Wisteria/BDEC-01(Odyssey)System (http://nkl.cc.u-tokyo.ac.jp/22w/WisteriaBDEC01.pdf) with Fujitsu/Arm A64FX (same architecture as that of “Fugaku” supercomputer) at the University of Tokyo, which is ranked 23rd in the Top500 list published in November 2022 (https://www.top500.org/).

Finite-Element Method is widely-used for solving various types of real-world scientific and engineering problems, such as structural analysis, fluid dynamics, electromagnetics, and etc. This lecture course provides brief introduction to procedures of FEM for 1D/3D steady-state heat conduction problems with iterative linear solvers and to parallel FEM. Lectures for parallel FEM will be focused on design of data structure for distributed local mesh files, which is the key issue for efficient parallel FEM. Introduction to MPI (Message Passing Interface), which is widely used method as "de facto standard" of parallel programming, is also provided.
Solving large-scale linear equations with sparse coefficient matrices is the most expensive and important part of FEM and other methods for scientific computing, such as Finite-Difference Method (FDM) and Finite-Volume Method (FVM). Recently, families of Krylov iterative solvers are widely used for this process. In this class, details of implementations of parallel Krylov iterative methods are provided along with parallel FEM.
Moreover, lectures on programming for multicore architectures will be also given along with brief introduction to OpenMP and OpenMP/MPI Hybrid Parallel Programming.
Prerequisites
-
Experiences in Unix/Linux (vi or emacs)
-
List of Unix/Linux Commands (Wikipedia)
-
https://en.wikipedia.org/wiki/List_of_Unix_commands
-
Onlie Manuarl for Emacs (Screen Editor for Linux/Unix)
-
https://www.gnu.org/software/emacs/manual/
-
Experiences in programming by Fortran or C/C++
-
Undergraduate-Level Mathematics and Physics (e.g. Linear Algebra, calculus)
-
Fundamental numerical algorithms (Gaussian Elimination, LU Factorization, Jacobi/Gauss-Seidel/SOR Iterative Solvers, Conjugate Gradient Method (CG))
-
Experiences in SSH Public Key Authentication Method (optional)
-
Participants are encouraged to read the following material, and to understand fundamental issues of the MWR (Method of Weighted Residual) before this course.
-
http://nkl.cc.u-tokyo.ac.jp/22w/02-FEM/FEMintro.pdf
Preparation for Personal Computer
2. Schedule
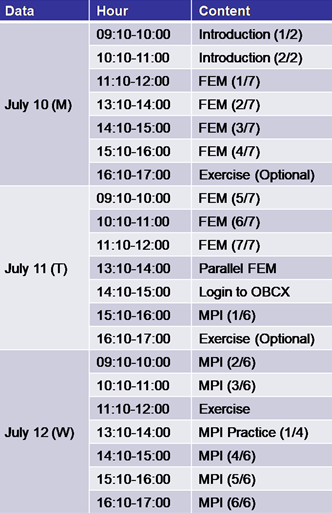
.png)
References
3. Course Outline & Descriptions
This 5-day intensive “in-person” class provides introduction to large-scale scientific computing using the most advanced massively parallel supercomputers. Topics cover:
-
Finite-Element Method (FEM)
-
Message Passing Interface (MPI)
-
Parallel FEM using MPI and OpenMP
-
Parallel Numerical Algorithms for Iterative Linear Solvers
4. Grading
Course attendance and hands-on coding
5. Registration (Deadline: June 15)
https://forms.gle/ebyVg2QK9QUTbNvj8
Contact:
Murphy Yu murphyyu@ncts.tw
Poster: events_3_283230511510466266.pdf
